Title: Multiresolution Analysis with Non-Nested Spaces (GP. Bonneau)

red line

Abstract:

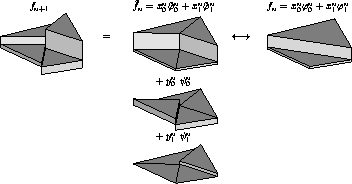
Two multiresolution analyses (MRA) intended to be used in scientific visualization, and that are both based on a non-nested set of approximating spaces, are presented. The notion of approximated refinement is introduced to deal with non nested spaces. The first MRA scheme, refered to as BLaC (Blending of Linear and Constant) wavelets is based on a one parameter family of wavelet bases that realizes a blend between the Haar and the linear wavelet bases. The approximated refinement is applied in the last part to build a second MRA scheme for data defined on an arbitrary planar triangular mesh .

Reference: Dagstuhl seminar on Geometric Design (1996)

red line

The concept of approximated refinement, and the ability to deal with a non-nested set of approximation spaces, enables to define wavelet coefficients corresponding to the suppression of vertices in a data set defined on an irregular triangulation.

approximated refinement

Schematical representation of the triangular wavelet decomposition.

Partial reconstructions of a data set defined on an irregular triangulation, using approximately 40% of the wavelet coefficients.

Original data set (48682 triangles).
original data set gziped-Ps (450Kb)

Partial reconstruction at a fixed level & corresonding triangular mesh (20006 triangles).
level reconstruction gziped-Ps (190Kb) level reconstruction gziped-Ps (190Kb)

Partial reconstruction using the bigest wavelet coefficients & corresponding triangular mesh (20580 triangles).
treshold reconstruction gziped-Ps (200Kb) treshold reconstruction gziped-Ps (200Kb)

Dot    Return to George-Pierre Bonneau's homepage.